Satz von Stiller: Unterschied zwischen den Versionen
Aus MünsterWiki
| Zeile 1: | Zeile 1: | ||
| − | [[Kategorie: | + | [[Datei:Pascal-6points-s.svg|300px|mini|Der [[Satz von Pascal]] an der mormalen Ellipse]] |
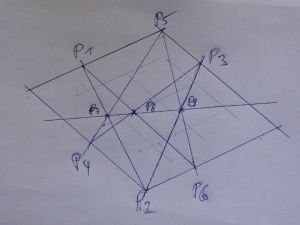
| + | [[Datei:Bild z 41.jpg|thumb|300px|Der Satz von Stiller am regelmäßigen Viereck (Parallelogramm)]] | ||
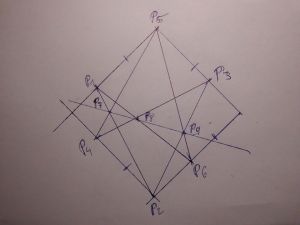
| + | [[Datei:Bild z 43.jpg|thumb|300px|left|Der Satz vin Stiller am Quadrat - alle drei Schnittpunkte liegen auf einer Geraden.]] | ||
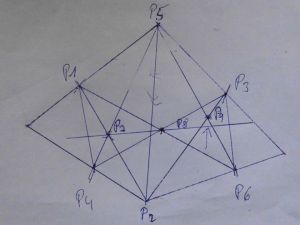
| + | [[Datei:Bild z 42.jpg|thumb|300px|Am unregelmäßigen Viereck geht es leider "nicht". P9 fällt aud der Geraden heraus.]] | ||
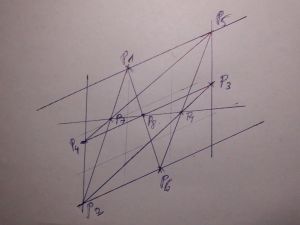
| + | [[Datei:Bild z 44.jpg|thumb|300px|left|Der Satz von Stiller noch einmal am Parallelo- gramm. Es geht "immer".]] | ||
| + | |||
| + | Der '''Satz von Stiller''' (nach [[Joachim Stiller]]) ist eine Aussage über ein 6-Eck auf einem regelmäßigen Viereck (Parallelogramm) in einer [[Projektive Ebene|projektiven Ebene]]. Er lässt sich in der reellen affinen Ebene wie folgt formulieren: | ||
| + | |||
| + | Für paarweise gegenüberliegende 6 Punkte <math>P_1,P_2,P_3,P_4,P_5,P_6 </math> eines regelmäßigen Vierecks (Parallelogramm) in einer projektiven Ebene liegen die Punkte | ||
| + | : <math> P_7:= \overline{P_1P_2}\cap \overline{P_4P_5},</math> | ||
| + | : <math> P_8:= \overline{P_6P_1}\cap \overline{P_3P_4},</math> | ||
| + | : <math> P_9:= \overline{P_2P_3}\cap \overline{P_5P_6}</math> | ||
| + | auf einer Geraden, der '''Stiller-Geraden''' (s. Bild unten). | ||
| + | |||
| + | [[Kategorie:Synthetische Geometrie]] | ||
| + | [[Kategorie:Projektive Geometrie]] | ||
| + | [[Kategorie:Satz (Mathematik)]] | ||
| + | [[Kategorie:Affine Geometrie]] | ||
| + | [[Kategorie:Ebene Geometrie]] | ||
| + | [[Kategorie:Joachim Stiller]] | ||
Version vom 16. Juli 2025, 13:17 Uhr
Datei:Pascal-6points-s.svg
Der Satz von Pascal an der mormalen Ellipse
Der Satz von Stiller (nach Joachim Stiller) ist eine Aussage über ein 6-Eck auf einem regelmäßigen Viereck (Parallelogramm) in einer projektiven Ebene. Er lässt sich in der reellen affinen Ebene wie folgt formulieren:
Für paarweise gegenüberliegende 6 Punkte <math>P_1,P_2,P_3,P_4,P_5,P_6 </math> eines regelmäßigen Vierecks (Parallelogramm) in einer projektiven Ebene liegen die Punkte
- <math> P_7:= \overline{P_1P_2}\cap \overline{P_4P_5},</math>
- <math> P_8:= \overline{P_6P_1}\cap \overline{P_3P_4},</math>
- <math> P_9:= \overline{P_2P_3}\cap \overline{P_5P_6}</math>
auf einer Geraden, der Stiller-Geraden (s. Bild unten).